Бесконечная сила. Как математический анализ раскрывает тайны вселенной - читать онлайн книгу. Автор: Стивен Строгац cтр.№ 58

Глубоко скрытые связи между этими идеями – наклоны и площади, кривые и функции, скорость изменения и производные – вышли из тени, когда Ньютон взглянул на них с динамической точки зрения. Поразмышляйте над приведенным выше графиком и представьте, что x двигается направо с постоянной скоростью. Вы можете даже думать об x как о времени: Ньютон часто так и делал. По мере движения x площадь серой области непрерывно меняется. Поскольку она зависит от x, ее следует рассматривать как функцию от x, так что запишем ее в виде A(x). Когда мы хотим подчеркнуть, что эта площадь является функцией x (в противопоставление фиксированному числу), мы будем называть ее функцией накопления площади, а иногда просто функцией площади.

Мой преподаватель анализа в старших классах, мистер Джоффри, предлагал яркую запоминающуюся метафору для этого «текучего» сценария, когда x скользит, а вместе с ним меняется площадь. Он просил нас представить волшебный малярный валик, который движется по горизонтали. Двигаясь вправо, он окрашивает в серый цвет участок под кривой.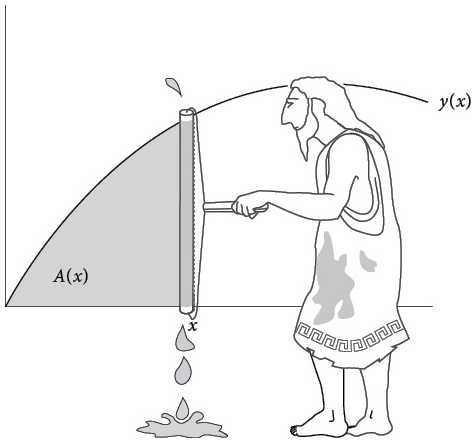

Пунктирная линия в точке x обозначает текущее положение этого воображаемого малярного валика, пока он двигается вправо. При этом для гарантии аккуратного окрашивания валик мгновенно каким-то волшебным образом растягивается или сжимается в вертикальном направлении – в точности от кривой вверху до оси x внизу, но их не пересекая. Волшебство тут в том, что валик при движении всегда меняет свою длину до величины y(x), чтобы безукоризненно окрашивать площадь нужной фигуры.

Сочинив такой неправдоподобный сценарий, зададимся вопросом: с какой скоростью серая площадь увеличивается по мере перемещения x вправо? Или, что эквивалентно, с какой скоростью ложится краска, когда малярный валик находится в точке x? Для ответа на вопрос подумайте, что произойдет в следующий бесконечно малый интервал времени. Валик перемещается вправо на бесконечно малый промежуток dx. Когда он проходит такое крошечное расстояние, его длина в вертикальном направлении практически не меняется, поскольку при столь бесконечно малом перемещении у него почти нет времени на изменение длины (этот тонкий момент мы обсудим в следующей главе). В течение этого короткого интервала валик фактически окрашивает высокий тонкий прямоугольник с высотой y и бесконечно малой шириной dx, бесконечно малая площадь которого равна dA = y dx. Разделив части этого уравнения на dx, мы получим скорость, с которой накапливается площадь. Она определяется соотношением

Эта аккуратная формула говорит, что общая окрашенная площадь под кривой увеличивается со скоростью, равной текущей высоте y малярного валика. Это логично: чем длиннее валик в данный момент, тем больше краски он наносит в следующее мгновение и тем быстрее накапливается окрашенная площадь.

Приложив еще немного усилий, мы могли бы доказать, что эта геометрическая версия теоремы эквивалентна версии с движением, которую мы использовали ранее, где утверждалось, что накопленная площадь под кривой скорости равна расстоянию, пройденному двигающимся телом. Однако у нас есть более срочные задачи. Нам нужно понять, что означает эта теорема, почему она так важна и как она в итоге изменила мир.

Значение основной теоремы

Следующая диаграмма подытоживает то, что мы только что узнали.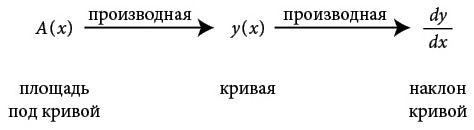

На ней показаны три функции, которые нас интересуют, и взаимосвязи между ними. Наша кривая находится в середине, ее неизвестный наклон – справа, а неизвестная площадь под ней – слева. Как мы видели в главе 6, именно эти три функции фигурируют в трех основных задачах анализа. Имея кривую y, мы пытаемся вычислить ее наклон и площадь.

Надеюсь, эта диаграмма проясняет, почему я назвал поиск наклона «прямой задачей». Чтобы найти наклон для кривой, мы просто следуем по стрелке вправо. Для определения наклона мы вычисляем производную y. Это прямая задача (1), которую мы обсуждали в предыдущей главе.

А вот чего мы не знали прежде, но узнали из основной теоремы сейчас, это то, что площадь A и кривая y тоже связаны производной: основная теорема гласит, что производная A – это y. Это потрясающий факт. Он позволяет нам определить площадь под произвольной кривой, решив тем самым древнюю задачу, почти две тысячи лет ставившую в тупик величайшие умы. Эта картинка подсказывает путь к ответу. Но прежде чем откупоривать шампанское, нужно осознать, что основная теорема дает нам не совсем то, что мы хотим. Она не дает нам непосредственно площадь, но рассказывает, как ее получить.

Святой Грааль интегрального исчисления

Как я уже пытался разъяснить, основная теорема не полностью решает задачу площади. Она предоставляет информацию о скорости ее изменения, но саму площадь нам еще нужно получить.

Языком символов основная теорема сообщает нам, что dA / dx = y, где y(x) – имеющаяся у нас функция. Однако нам по-прежнему нужно найти A(x), удовлетворяющее этому уравнению. Погодите минутку! Это же означает, что мы внезапно снова столкнулись с обратной задачей! Вот так поворот! Мы пытались решить задачу площади, центральную задачу номер 3 в списке из главы 6, и вдруг столкнулись с обратной задачей, центральной задачей номер 2 в том же списке. Я называю ее обратной задачей, потому что, как показывает диаграмма выше, поиск A по y означает движение против стрелки, движение назад относительно производной. В этом случае детская игра может выглядеть примерно так: «Я задумал функцию площади A(x), производная которой равна 12x + x¹⁰ – sinx. Какую функцию я задумал?»

Разработка метода решения обратной задачи – не только для 12x + x¹⁰ – sinx, но и для произвольной кривой y(x) – стала святым Граалем для анализа. Точнее, святым Граалем для интегрального исчисления. Решение обратной задачи позволило бы раз и навсегда закрыть тему нахождения площади. Имея y(x), мы бы знали площадь A(x) под ней. Решив обратную задачу, мы бы также решили задачу площади. Именно это я имел в виду, когда говорил, что эти две задачи – близнецы, разлученные при рождении. Это две стороны одной медали.