Искусство мыслить рационально. Шорткаты в математике и в жизни - читать онлайн книгу. Автор: Маркус Дю Сотой cтр.№ 11

Чуть более систематическим будет следующий подход. Начнем с одних лишь одинарных шагов. С ними решение только одно: 1111111111. Затем добавим к одинарным шагам один двойной. Тогда нужно сделать в общей сложности девять шагов – восемь одинарных и один двойной, причем каким по счету будет двойной шаг, можно выбирать. Этот двойной шаг можно сделать в девяти разных местах.

Эта стратегия кажется перспективной. На следующем этапе можно рассмотреть комбинации с двумя двойными шагами, перемешанными с шестью одинарными. В этом варианте подъем совершается за восемь шагов. Но придется вычислить, сколько существует вариантов выбора, то есть какой из восьми шагов будет двойным. Один двойной шаг можно сделать в восьми разных местах, а второй – в семи оставшихся после первого. Создается впечатление, что число возможных вариантов – 8 × 7. Но тут нужно действовать осторожно, потому что на самом деле мы учли одни и те же варианты дважды. Можно назначить первый двойной шаг на положение № 1, а второй – на положение № 2, а можно сделать наоборот. Результат от этого не изменится. Поэтому суммарное число возможных вариантов равно (8 × 7)/2 = 28. Собственно говоря, у этого числа есть особое математическое название. Оно называется числом сочетаний из 8 по 2 и обозначается следующим образом ^[20]: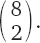

В более общем случае число вариантов выбора двух чисел из N + 1 чисел вычисляется по формуле 1/2 N(N + 1) – той же самой формуле, которую Гаусс использовал для треугольных чисел. Снова то же самое колесо, которое мы уже изобрели! Задачу о выборе двух чисел из N + 1 действительно можно свести к задаче вычисления треугольных чисел. В главе 3 я покажу, каким прекрасным шорткатом к решению одной задачи часто может быть ее преобразование в другую.

Эти инструменты для вычисления количества вариантов выбора, называемые биномиальными коэффициентами, были и в числе тех формул, которые Гаусс и помощник его учителя Бартельс вместе разбирали в своих книгах по алгебре.

Но чтобы решить нашу головоломку, на следующем этапе нужно вычислить, какими способами можно выбрать три места для трех двойных шагов по лестнице из семи возможных. Хотя этот метод кажется разумным и систематическим, нам нужно будет придумывать все новые формулы для включения в подъем по лестнице все большего числа двойных шагов. Эта работа начинает казаться трудоемкой и медленной – совсем не такой, каким должен быть шорткат.

Поэтому я опишу более удобный способ, основанный на том, о чем я рассказывал в этой главе. Очень действенной стратегией для решения таких головоломок мне кажется следующая: нужно рассмотреть малое количество ступенек и выяснить, есть ли в получающихся для них числах какой-нибудь паттерн.

Вот все варианты для лестниц из 1, 2, 3, 4 и 5 ступенек, которые можно быстро перебрать вручную:

Последовательность количества вариантов выглядит так: 1, 2, 3, 5, 8… Возможно, вы уже заметили паттерн. Следующее число получается сложением двух предыдущих. Возможно, вы даже знаете, как называются эти числа. Это же числа Фибоначчи! Они названы в честь математика XII века, открывшего, что эти числа – ключ к процессам роста природных объектов. Цветочных лепестков, сосновых шишек, ракушек, популяций кроликов. Все эти числа, по-видимому, следуют одному и тому же паттерну.

Фибоначчи открыл, что процессы роста в природе следуют одному простому алгоритму. Правило сложения двух предыдущих чисел – это шорткат природы к созданию сложных структур, например ракушек, шишек или цветков. Каждый организм использует две последние созданные им вещи в качестве ингредиентов для следующего шага.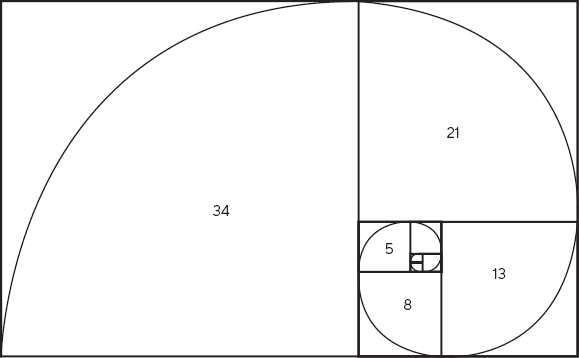

Рис. 1.4. Построение спирали при помощи чисел Фибоначчи

Использование паттернов в развитии структур – ключевой шорткат природы. Взять, например, тот способ, которым природа создает вирус. Вирусы обладают чрезвычайно симметричной структурой. Связано это с тем, что алгоритм создания симметричной структуры прост. Если вирус имеет форму симметричного кубика, то ДНК, которая воспроизводит эту молекулу, нужно создать лишь несколько экземпляров одного и того же белка, образующего грани кубика, а затем вся структура вируса может быть построена по тому же правилу. Никакие особые инструкции для разных граней не требуются. Паттерн позволяет строить вирус быстро и рационально, что и делает его таким смертельно опасным.

Но можем ли мы быть уверены, исходя из столь малого количества данных, что секрет подъема по лестнице действительно скрыт в числах Фибоначчи?

На самом деле правило точно объясняет, как вычислить количество вариантов для следующего этапа, лестницы из 6 ступенек. Нужно взять все возможные варианты для четырех ступенек и прибавить в конце по двойному шагу. Или взять все возможные варианты для пяти и прибавить к ним по шагу одинарному. Это дает все возможности для шести ступенек. Получается сочетание двух предыдущих чисел последовательности.

Чтобы получить ответ на исходную головоломку, нужно вычислить десятый член последовательности.

Существует 89 разных вариантов. Этот паттерн – шорткат к вычислению количества возможных способов подъема до вершины лестницы. И этот же паттерн позволяет решить эту задачу, даже если ступенек будет 100 или 1000.

Хотя эти числа названы в честь Фибоначчи, первым их открыл не он. Это были индийские музыканты, игравшие на табла ^[21]. Они издавна состязались друг с другом, щеголяя разными ритмами, которые им удавалось извлекать из своих барабанов. По мере исследования разных типов ритмов, которые получались из долгих и кратких тактов, они и пришли к числам Фибоначчи.

Если долгий такт в два раза длиннее краткого такта, то количество ритмов, которые может составить из них музыкант, играющий на табла, будет таким же, что и количество вариантов подъема по лестнице. Каждый одинарный шаг соответствует краткому такту, а каждый двойной шаг – долгому. Значит, число возможных ритмов определяется правилом Фибоначчи. Более того, это же правило дает музыканту алгоритм построения новых ритмов из уже существующих более коротких.